PEFT - Adapter Tuning

Perameter efficient finetuning using Adapters

Large pre-trained language models (e.g., BERT, GPT) have revolutionized NLP tasks by leveraging massive amounts of unlabeled data. Transfer learning involves first pre-training these models on large corpora and then fine-tuning them on smaller, task-specific datasets. However, fine-tuning all the parameters of a model like BERT is computationally expensive and inefficient, particularly when there are multiple downstream tasks

Adapter Layers

• Adapters are small, task-specific layers added between the layers of the pre-trained model.
• Instead of fine-tuning all the parameters of the model, only the parameters of the adapter layers are updated during training for a specific task. The rest of the model’s parameters remain frozen.
• This method significantly reduces the number of trainable parameters and, thus, the computational cost of fine-tuning.

Basic Adapter Design

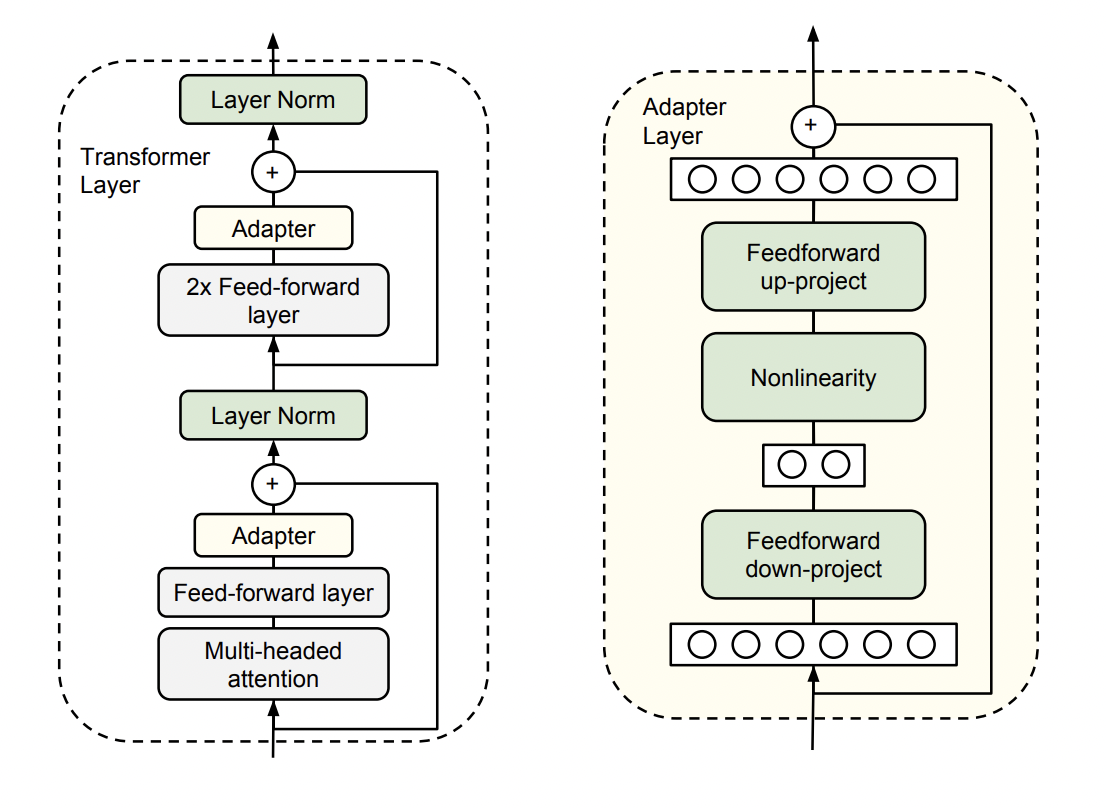
• Each adapter consists of a down-projection, a non-linearity, and an up-projection as shown in above image
• The down-projection reduces the dimensionality of the intermediate layer activations, and the up-projection restores it, thus keeping the adapter small and efficient.
• The adapters first project the original d-dimensional features into a smaller dimension, m, apply a nonlinearity, then project back to d dimensions.
• so The total number of parameters added per layer, including biases, is 2md + d + m.
• By setting m << d, we limit the number of parameters added per task.

Adapter Fusion

• Sequential fine-tuning and multi-task learning are methods aiming to incorporate knowledge from multiple tasks; however, they suffer from catastrophic forgetting and difficulties in dataset balancing.
• AdapterFusion addresses this by non-destructively composing multiple tasks. Rather than overwriting model parameters for each task, the method fuses information from different adapters to solve a new task.
• algorithm:
  • train a adapter layers for each task seperatly.
  • AdapterFusion learns a weighted combination of previously trained all adapters as shown in below figure.

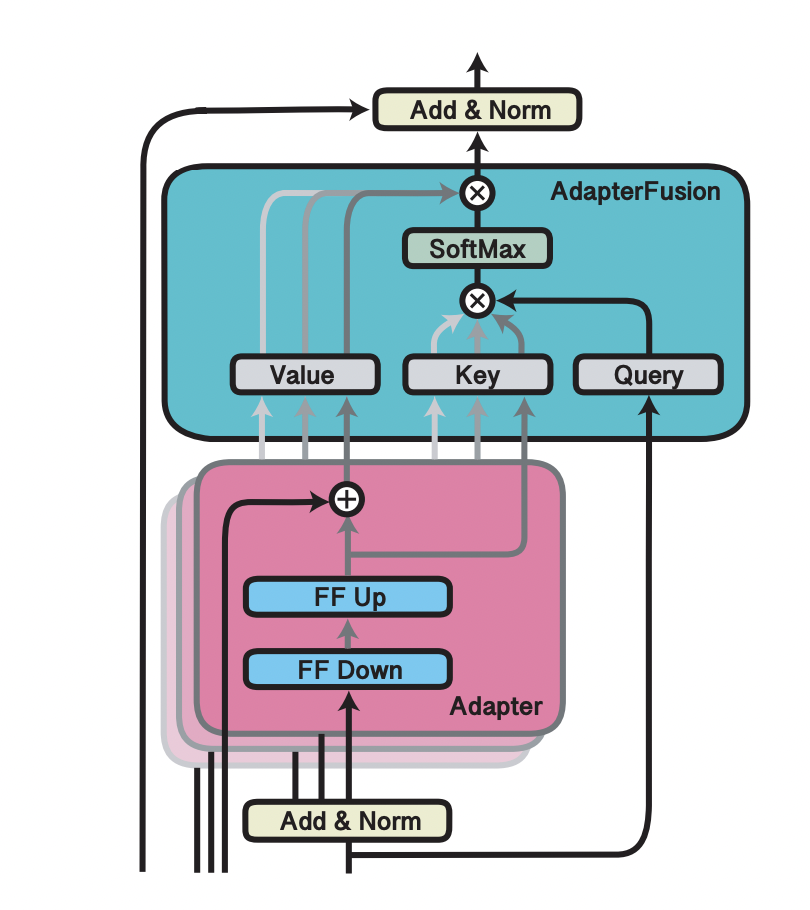
• This fusion mechanism allows the model to leverage knowledge from all tasks in a modular fashion.
• The adapters themselves remain independent, and the fusion weights can be tuned to emphasize adapters that are most relevant for a specific task.

COMPACTER (Compact Adapter)

COMPACTER is combination of Hypercomplex Adapter Layers using Kronecker Product, Low-Rank Approximation, shared weights across adapters.

Kronecker Product:

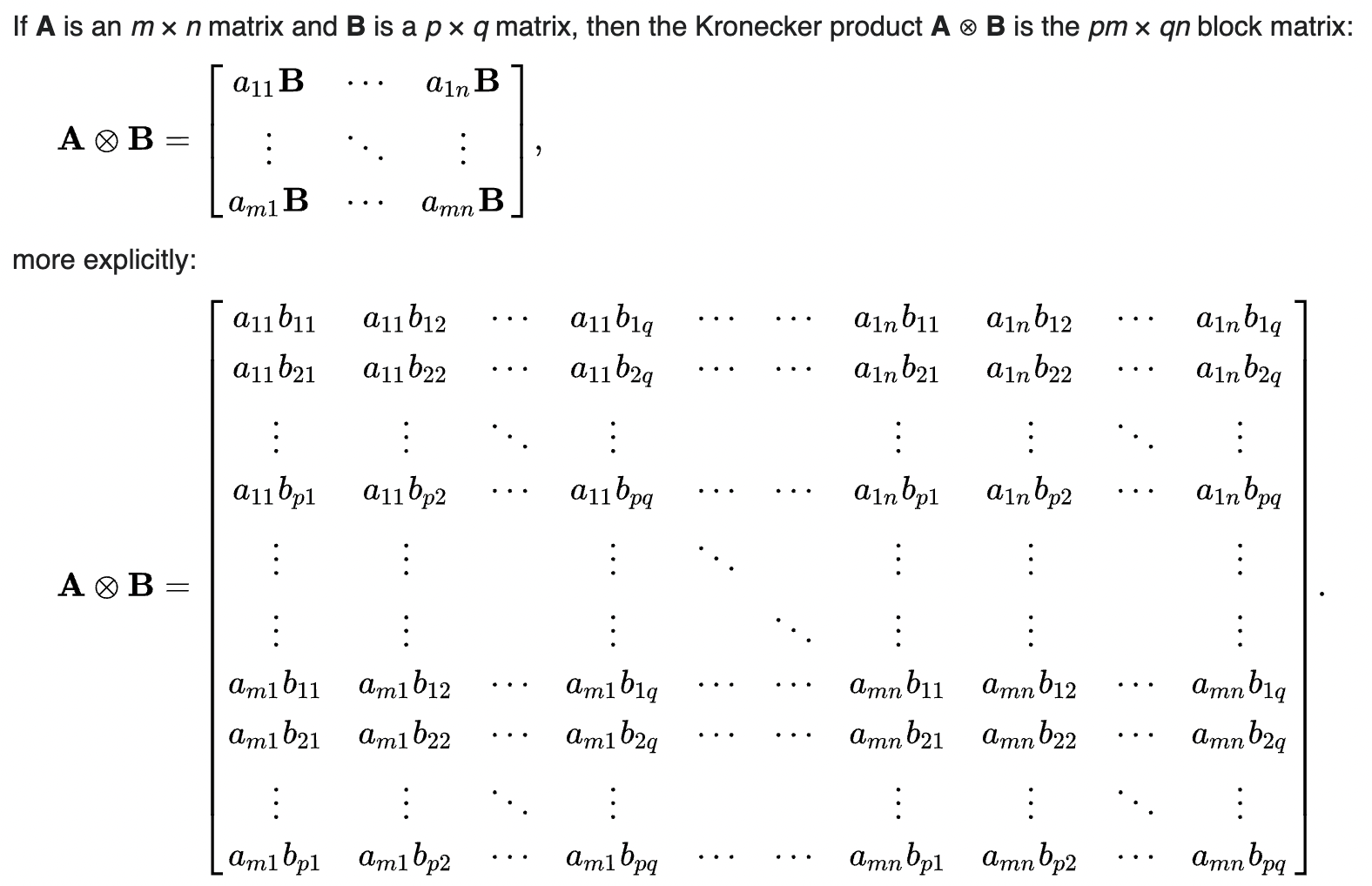
Hypercomplex Adapter Layers:

In the adapter layers, previously it used the FC layers as below

\[\begin{align} y = Wx + b \quad \text{where } W \text{ is } (m \times d)\\ \end{align}\]

W will be replaced using Kronecker Product of two matrices like below

\[\begin{align} W = \sum_{i=1}^n A_i \otimes B_i \\ A_i \text{ is } (n \times n) \quad , \quad B_i \text{ is } (\frac{m}{n} \times \frac{d}{n}) \\ \end{align}\]

n is user defined hyper-parameter. d, m are must divisible by n

Below is the illustration of Hypercomplex Adapter Layers. It is sum of Kronecker Product of matrices \(A_i\), \(B_i\) and here n = 2, d = 8, m = 6

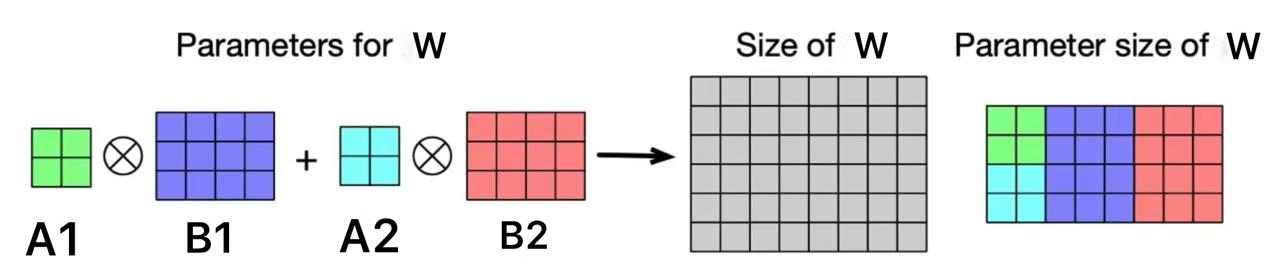
No of parameters to tune here is reduced compared to FC layer as shown above.

This layer is generalization of the FC layer via the hyperparameter n. 

• when n = 1, \(W = A_1 \otimes B_1 = aB_1\) (a is the single element of the 1×1 matrix), B1 matrix is of shape \(m \times d\)
• Since learning a and \(B_1\) separately is equivalent to learning their multiplication jointly, scalar a can be dropped, which is learning the single weight matrix in an FC layer

Low Rank Parameterization and Sharing information across adapters

• \(A_i\) are shared parameters that are common across all adapter layers while \(B_i\) are adapter-specific parameters.
• assumption is the model can also be effectively adapted by learning transformations in a low-rank subspace and \(B_i\) is divided into multiplication of two low rank matrices

\[\begin{align} W = \sum_{i=1}^n A_i \otimes B_i = \sum_{i=1}^n A_i \otimes (s_i t_i)\\ s_i \text{ is } (\frac{m}{n} \times r) \quad t_i \text{ is } (r \times \frac{d}{n}) \quad \text{matrix} \end{align}\]

Reference:

1. https://arxiv.org/pdf/1902.00751
2. https://arxiv.org/pdf/2005.00247
3. https://arxiv.org/pdf/2102.08597